Let there be n boxes and n1 objects. The Pigeonhole principle can sometimes help with this. what is extended pigeonhole principle.
What Is Extended Pigeonhole Principle, A basic version says that if N1 pigeons occupy N holes then some hole must have at least 2 pigeons. Answer 1 of 7. Then under any assignment of objects to the boxes there will always be a box with more than one object in it.
 The Pigeonhole Principle Alan Kaylor Cline The Pigeonhole From slidetodoc.com
The Pigeonhole Principle Alan Kaylor Cline The Pigeonhole From slidetodoc.com
Answer 1 of 7. Greatest integer function or floor function is explained with. The pigeonhole principle also known as the Dirichlet principle originated with German mathematician Peter.
Pigeonhole principle is one of the simplest but most useful ideas in mathematics.
Another definition could be phrased as among any integers there are two with the same modulo- residue. An alternate more generalized version is. We use a proof by contraposition. Then S x S y nq x. S and n remainders modulo n by the pigeonhole principle there must be at least two S k s that leave the same remainder modulo n.
Another Article :

If there are rn1 pigeons and n pigeonholes then at least one pigeonhole will have more than. 2 For a nonempty finite collection of integers not necessarily distinct the maximum value is at least the average value. Let two of these S k s be S x and S y withx y and let the remainder be r. Suppose none of the k boxes contains more than one object. Answer 1 of 7. Pigeon Hole Principle Discrete Math Niharika Panda Youtube.

Since S x n r there exists q x ℤ such that S x nq x r. As Dijkstra remarked this is in some sense equivalent to the notion that for a finite set of numbers the maximum value is. Greatest integer function or floor function is explained with. Suppose none of the y boxes has more than one object then the total number of objects would be at most y. Then some box contains at least two objects. Todays Topics Counting Generalized Pigeonhole Principle Permutations Combinations.

The pigeonhole principle is one of the simplest but most useful ideas in mathematics and can rescue us here. An alternate more generalized version is. It states that if n pigeons are assigned to m pigeonholes The number of pigeons is very large than the number of pigeonholes then one of the pigeonholes must contain at least n-1m1 pigeons. Suppose none of the k boxes contains more than one object. Of pigeons per pigeon hole. Basic Pigeon Hole Principle Problems Youtube.

So the total number of objects would be at most k. Discretemathematics discretestructure dim dis lmt lastmomenttuitions Second YearTo get the study materials for final yeatNotes video lectures prev. This is actually an application of the pigeonhole principle which we now state. Prims and Dijkstras Minimal spanning Tree 10 min. We use a proof by contraposition. Ppt Unit 2 6 Pigeonhole Principle Powerpoint Presentation Free Download Id 2435237.

Since S x n r there exists q x ℤ such that S x nq x r. Average number of pigeons per hole Kn1n K 1n. Prims and Dijkstras Minimal spanning Tree 10 min. Pigeonhole and Extended Pigeonhole Principle 08 min. Theorem 161 Pigeonhole Principle Suppose that n 1 or more objects are put into n boxes. Pigeonhole Principle In Any Cocktail Party N J2 People There Must Be At Least Two People Who Have The Same Number Of Friends Assuming That The Friends Relation Is Symmetric And Irreflexive.

Answer 1 of 7. Similarly since S y n r there exists q y ℤ such that S y nq y r. So there is at least one box containing two or more of the objects. Discretemathematics discretestructure dim dis lmt lastmomenttuitions Second YearTo get the study materials for final yeatNotes video lectures prev. So the total number of objects would be at most k. Ppt Unit 2 6 Pigeonhole Principle Powerpoint Presentation Free Download Id 2435237.

An alternate more generalized version is. Find the minimum number of students in a class to be sure that three of them are born in the same month. As Dijkstra remarked this is in some sense equivalent to the notion that for a finite set of numbers the maximum value is. If there are rn1 pigeons and n pigeonholes then at least one pigeonhole will have more than. S and n remainders modulo n by the pigeonhole principle there must be at least two S k s that leave the same remainder modulo n. Pigeonhole Principle Defined W 11 Step By Step Examples.

Pigeonhole Principle and Extensions Pigeonhole Principle and Extensions The Pigeonhole Principle is one of almost obvious mathematical concepts which are both simple and powerful. Extended pigeonhole principle and examples are explained to help students in exam preparation. Extended Pigeonhole Principle EPP If nk1 objects are placed in n boxes then one of the boxes must contain at least k1 objects. So there is at least one box containing two or more of the objects. Theorem 1 The Pigeonhole Principle. 3 Counting Permutations Combinations Pigeonhole Principle Elements Of Probability Recurrence Relations Ppt Download.

Find the minimum number of students in a class to be sure that three of them are born in the same month. S and n remainders modulo n by the pigeonhole principle there must be at least two S k s that leave the same remainder modulo n. Pigeonhole principle is one of the simplest but most useful ideas in mathematics. Let two of these S k s be S x and S y withx y and let the remainder be r. Find the minimum number of students in a class to be sure that three of them are born in the same month. Pigeonhole Principle Defined W 11 Step By Step Examples.

This is actually an application of the pigeonhole principle which we now state. 1 If m objects are put in n boxes and n m then at least one box contains at least ceil mn objects. Assume k1 or more objects are placed into k boxes. - If n pigeonholes are occupied by kn1 or more pigeons where k is a positive integer then at least one pigeonhole is occupied by k1 or more pigeons. Suppose none of the k boxes contains more than one object. Generalized Pigeonhole Principle Discrete Maths Niharika Panda Youtube.

1 If n m pigeons are put into m pigeonholes theres a hole with more than one pigeon. Then the total number of objects is at most 1 1 1 n a contradiction. Then S x S y nq x. Generalized pigeonhole principle is. It states that if n pigeons are assigned to m pigeonholes The number of pigeons is very large than the number of pigeonholes then one of the pigeonholes must contain at. Ppt Unit 2 6 Pigeonhole Principle Powerpoint Presentation Free Download Id 2435237.
This is actually an application of the pigeonhole principle which we now state. Then under any assignment of objects to the boxes there will always be a box with more than one object in it. Kruskals Minimal spanning Tree 09 min. Then the total number of objects is at most 1 1 1 n a contradiction. The Extended Pigeonhole Principle. Condor Depaul Edu.

Since S x n r there exists q x ℤ such that S x nq x r. Pigeonhole principle proof. Let us first write all the numbers from 1 to 9 as said in the question 123456789 Now lets take any 5 numbers from 1 to 9 such as 13478 As it given that any two of the numbers out of the 5 numbers we have chosen should be equal to. 1 If n m pigeons are put into m pigeonholes theres a hole with more than one pigeon. Similarly since S y n r there exists q y ℤ such that S y nq y r. Prove The Extended Pigeonhole Principle With Induction Mathematics Stack Exchange.

The pigeonhole principle also known as the Dirichlet principle originated with German mathematician Peter. Another definition could be phrased as among any integers there are two with the same modulo- residue. Find the minimum number of students in a class to be sure that three of them are born in the same month. X rightarrow Y then there are at least k 1 distinct members x_1 dots x_k 1 in X such that fx dots fx_k1. If Kn1 pigeons are kept in n pigeon holes where K is a positive integer what is the average no. Solved 7 The Extended Pigeonhole Principle States That If K Chegg Com.
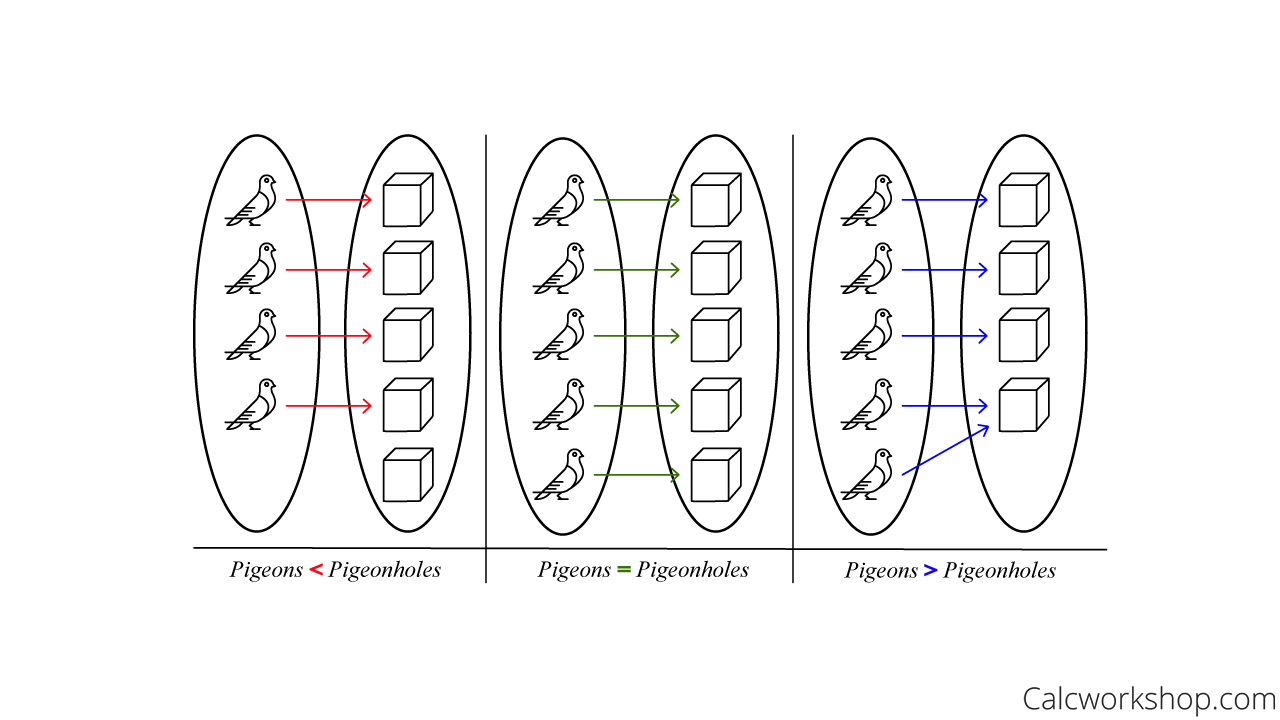
A basic version says that if N1 pigeons occupy N holes then some hole must have at least 2 pigeons. We will see more applications that proof of this theorem. Suppose none of the y boxes has more than one object then the total number of objects would be at most y. We use a proof by contraposition. The Pigeonhole principle can sometimes help with this. Pigeonhole Principle Defined W 11 Step By Step Examples.










